钱七虎1 ,陈士海1 ,2
(1 . 解放军理工大学 ,江苏南京 210007 ;2 . 山东科技大学 ,山东泰安 271019)
摘 要: 爆破地震震动达到足够强度时 ,就会引起各种破坏现象。寻找爆破地震烈度工程标准参数 ,研究爆破地震动强度 ,分析爆破地震力对结构的破坏作用 ,是当前工程结构抗爆破地震效应研究的重点问题。综述了爆破地震烈度的局限性 ,说明了爆破地震加速度和速度间的相关性 ,重点通过分析单质点系的爆破地震 反应 ,计算了结构中的内力 ,进而判断结构的破坏情况 ,得出建筑结构的震害是由爆破地震运动的加速度或速度最大值决定 ,而岩土工程的震害主要由地面运动最大速度决定的结论。
反应 ,计算了结构中的内力 ,进而判断结构的破坏情况 ,得出建筑结构的震害是由爆破地震运动的加速度或速度最大值决定 ,而岩土工程的震害主要由地面运动最大速度决定的结论。

关键词: 爆破地震; 建筑结构; 岩土工程; 烈度; 震害
1 引 言
爆破地震与天然地震有显著的差异。爆破地震有如下的特点:
1) 幅值高 ,衰减快。目前世界上记录到的天然地震加速度最大值仅为数 g , 而在大爆破的近区测
2) 震动频率高。天然地震震动的加速度的主频率大都在 2~5 周/ s ,很少超过 10 周/ s ,但爆破地震动的加速度主频率大都在 10 ~30 周/ s , 有的高达50 周/ s 。与普通工程结构的自振(基振) 频率相比 ,前者与它相接近 ,后者则比它高得多。
3) 持续时间短。爆破地震的主震段持续时间一得的加速度高达 25. 3 g 。但是爆破震动衰减很快, 破 般不超过 0 . 5 s ,短者小于 0 . 1 s ,比天然地震要短的坏区范围很小。
天然地震加速度最大值平均为0 . 1 g 时, 一般会造成房屋一定程度的破坏, 而爆破地震加速度值为1 . 0 g 时, 才会引起房屋的轻微破坏, 这与爆破地震的频率高、持续时间短、幅值衰减快等特点有很大的关系。
爆破地震效应的研究重点是: 1) 地震震动随药量、爆心距、地震震动传播的介质和场地条件而变化的规律;2) 地震震动的强度 ,即爆破地震破坏力的大小对建筑物的影响;3) 降低地震动强度的措施。
2 爆破地震震级和烈度
2 . 1爆破地震的震级
天然地震震级 M 表示地震本身大小的尺度。
M= log A
A 是标准地震仪在距震中 1 000 km 处纪录的以μm ( 10 - 4 ) 为单位的最大水平地动位移。如 A =10 mm = 104μm , 则 M = log104 = 4 , 即为4 级地震。
粗略估算一般工程爆破地震震级的经验公式为M= 3 . 65 + log Q Q 为药量, kt 。
如江西永平铜矿 , 1978 年 12 月 6 日进行了 1次 985 . 7 t 硝铵炸药爆破 ,则 M = 3 . 64 。
2 . 2爆破地震的烈度
地震烈度是地震时一定地点的地面震动强弱程度的尺度 ,是该地点一定范围内地面震动强度的平均水平[ 1 ] 。
2 . 3地震烈度表的局限性
在实际地震现场震害考察中 ,发现与单一物理量相对应的地震烈度表有不少矛盾。
爆破地震中 ,一些地震震动的最大水平加速度虽然高达 0 . 2~0 . 7 g ,但由于地震震动的持续时间很短 ,仅仅几秒钟 ,震害不重 ,烈度不高; 相反 ,一些地震震动最大水平加速度虽然多在 0 . 2 g 以下 ,但由于地震震动的持续时间长达 20~30 s 以上 ,震害严重 ,烈度较高。
因此 ,影响建筑物的地震震动参数至少应包括地震动的幅值、频谱和震动持续时间 3 个主要参数。
但是 ,天然地震的发生地点、时间和大小很难准确预测 ,因而仍保留烈度的概念。
而在爆破地震效应的研究中 ,这方面有有利条件:爆破震源的大小和位置以及作用方向可以控制 ,爆破震动的延续时间可以知道 ,爆破震动对结构的效应可以进行控制。因此在爆破地震效应的研究中 ,可抛弃应用预测地震震动强度的经验公式和不足以表征建筑物破坏特征的烈度工程标准 ,而直接代之以动力分析方法。
3 爆破地震震动的工程参数
3 . 1爆破地震工程参数的选择标准
在工程中选用地面震动的什么参数来表示地面震动的特征 ,主要决定于什么参数对建筑结构和构筑物的破坏起主要作用。
作为烈度工程标准的参数 ,可以用下列 3 条鉴别标准来选择:1) 它是决定爆破地震破坏力的主要因素 ,和宏观烈度有良好的相关性;2) 它与药量和爆心距有较好的相关性;3) 能用简单的仪器来测定。
总起来说 ,
1) 地震动峰值比较能全面满足 3 条标准;
2) 单一的地震动物理量不可能完善地代表宏观裂度 ,但想把地面震动的幅度、频率和震动持续时间3 个参数都纳入到烈度工程标准的定义中是困难的;
3) 宏观裂度是反映震害现象的。震害现象决定于工程结构物和构筑物对地面震动的反应 ( 效应) ,它不仅决定于地面震动的特征 ,而且决定于千变万化的工程结构的特征。例如高大烟囱、高塔结构的破坏主要受低频部分震动强度的影响 ,而低矮房屋的破坏主要受较高频部分震动强度的影响 ,而重型设备的移动主要受震动脉冲总量的影响。地面震动的峰值、频率和持续时间三因素的影响大小也随工程结构特性而异 ,随工程结构的破坏程度而异。
3 . 2地面震动峰值中地面加速度和速度的峰值
1) 爆破地震加速度峰值和速度峰值之间存在较好的相关性(图 1) ( 以二次实际爆破测量的爆破震动记录为例) ,可表示为
V= τa
应用回归分析 ,分别得回归系数和相关系数。
τ = 8 . 45 ×10 - 1 γ = 0 . 958
式中, a 为地震动最大加速度, m/ s² ; V 为地震震动最大速度, cm/ s 。
2) 加速度和速度的比较
加速度的优点是能和地震产生的惯性力相联系 ,可以直接从加速度记录量出 ,便于作用于建筑物的爆破地震荷载的换算 ,从而进行建筑物的应力分析。
利用速度的优点是能和地震波所携带的能通量所产生的地应力相联系 ,并和岩土工程构筑物的应力分析相系。
所以 ,加速度和速度各有优点。
3 . 3衡量定量地震烈度工程标准
根据大量爆破地震速度观测数据来看 ,爆破地震动的垂直向速度常常不是最大 ,而径向速度往往比较大;在爆心距较小时 ,径向与垂直向加速度同一量级 ,在远离爆心时 ,地震震动以径向加速度为主。且由于建筑物在竖向远比水平向具有较强的抗震能力 ,所以把水平向最大速度值或最大加速度值作为地震动烈度的物理标准比较适宜。
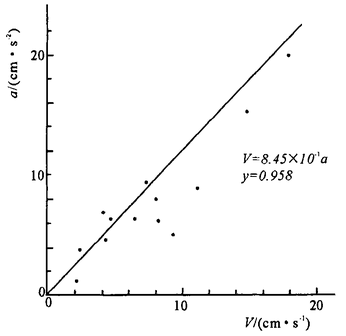
图1爆破地震震动最大加速度与最大速度之间的关系
4 爆破地震震动强度的预测
爆破时 ,影响地震动强度的因素很多 ,主要包括爆源变量: 药量、埋深、爆源介质物理参数、爆破方式、放置炸药的孔硐的自然性质等等 ,以及传播途径的变量:爆心距、传播途径的地质背景、岩土条件等。要完全考虑这些变量是困难的 , 可近似地选择炸药量 Q 和爆心距 R 作为主要变量, 其它变量归纳到常系数中去。
震动幅值: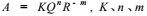 为常系数。
为常系数。
我国常用的为苏联萨道夫斯基经验公式:
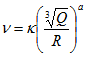
抛掷爆破时为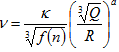 ,K,a为岩石特性等因素有关的常数 ,采用地震动最大加速度的经验公式亦为 ,
,K,a为岩石特性等因素有关的常数 ,采用地震动最大加速度的经验公式亦为 , 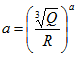 。
。
原苏联和我国各单位的经验系数值 K ,α变化很大。
实际应用时, 宜在爆破现场进行小当量预先试爆, 整理观测数据, 用回归分析的方法或紧绳法整理得出 K , α 。
5 爆破地震效应的建筑结构反应和爆破地震荷载
爆破时 ,建筑结构的破坏决定于爆破地震效应引起的建筑结构反应(位移和内力) 的大小。因此 ,要充分理解爆破地震破坏的烈度工程标准 ,必须研究爆破地震效应引起的建筑结构反应。
5 . 1单质点系的爆破地震反应以烟囱为例来说明。烟囱如何受力 ,如何破坏的 ,与哪些因素有关。爆破地震烈度工程标准应该如何确定 ?
为了分析简单起见 ,先分析单质点的爆破地震反应(如图 2)
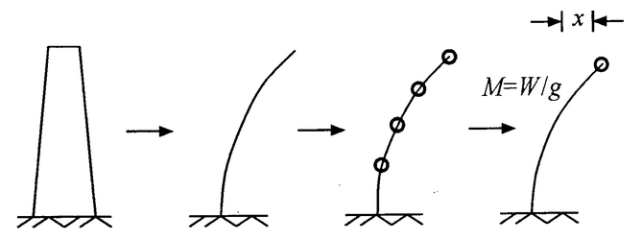
图 2 烟筒模型简化的单质点爆破地震反应示意图
由于爆破地震的运动 ,引起烟囱震动 ,研究烟囱震动
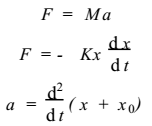
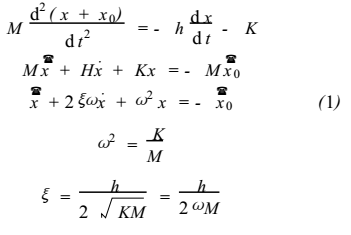
1) 是单质点系在地震地面运动影响下的运动方程 , x 0 是地面运动位移。地震效应发生前地面静止 ,则方程的积分为
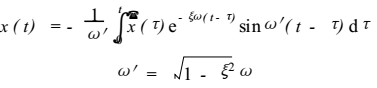
经过简单运算,可得体系的相对速度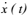 和绝对加速度
和绝对加速度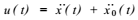 分别为
分别为
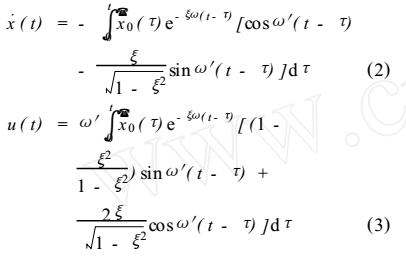
一般情况下,结构的阻尼比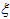 很小
很小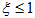 ,则在式(2)、式(3)中略去
,则在式(2)、式(3)中略去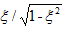 和
和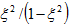 项,并取
项,并取 ,得到:
,得到:

实际上,公式(4)可转化为:
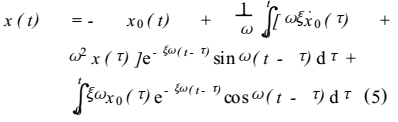
公式(1)也可以化成用速度激励的方程形式:

方程(6)的解显然可用杜哈姆积分求出:
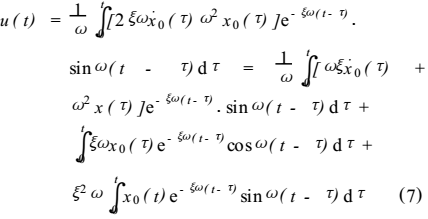
去掉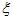 的高次项
的高次项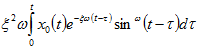 ,从而,在速度荷载激励下结构的相对位移为:
,从而,在速度荷载激励下结构的相对位移为:


(5) 式、(8) 式说明 2 种激励下的相对位移相同 ,同时地震荷载也是相同的。
通过慢变函数解法 ,在忽略ξ的高次项情况下 ,质量 M 在爆破地震运动作用下 ,其最大相对位移、速度和绝对加速度可近似用下式表示:
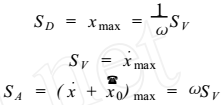
于是 ,作用在单质点结构上的最大惯性力 ,即地震力为:
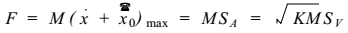
也可以写成如下形式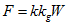

有了地震力、地震荷载以后 ,就可以求出结构中的内力。有了内力可求出结构中的应力 ,从而与结构材料的应力强度极限相比 ,判断出结构是否破坏。
结构地震震害( 烈度) 由地震力所决定。因此,它由爆破地震运动的加速度最大值或速度最大值和Kg 的最大值决定。
Kg 的值由结构特性ω以及 ¨x( t ) 的参数( 地运动延续时间以及波形, 因而地运动的频率特性) 所决定, 体现出爆破地震动幅值、持续时间和频率特性的影响。它的值可由一个小于 1 的值到 3 之间变化。
对于地面震动速度荷载 ,同样采用慢变函数解法 ,会得到用速度荷载表征的爆破地震荷载:

式中 , 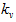 为速度地震动系数;
为速度地震动系数; 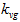 为速度动力系数。
为速度动力系数。
无论采用什么类型的地震动荷载 ,由于结构震动响应( 包括地震荷载) 与激励荷载的频率密切相关 ,还与震动的持续时间有关系 ,这样在表征结构爆破地震荷载大小时 ,应涉及各种荷载的幅值、频率和持续时间 ,因此无论对加速度荷载 ,还是速度荷载 ,单采用其峰值表征地震荷载是不全面的。
对应于具有确切爆破地面震动加速度峰值、频率和持续时间的荷载曲线 ,考虑速度与加速度荷载曲线间的微积分关系 ,即其震动曲线丰富的信号信息能够复制的话 ,必有确定的爆破震动速度峰值、频率及其持续时间。从这个意义上讲 ,采用爆破地震的震动速度或加速度的特征参数评判结构的动态响应与破坏都是最佳的。
5 . 2 多质点系的爆破地震反应
多质点系振型有一个振型分解问题[ 2 ] ( 图 3) ,其它就同单质点系的振动。
作用在 i 个质点上的地震荷载为
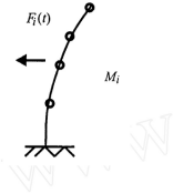
图 3 多质点系的爆破地震反应
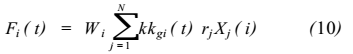
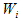 是第 i 个质量的重量; K 是地震系数;
是第 i 个质量的重量; K 是地震系数; 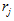 是振型分解系数。
是振型分解系数。
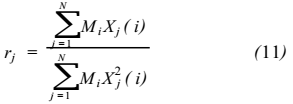
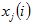 第 j 个振型 i 点处相对位移的值。
第 j 个振型 i 点处相对位移的值。
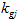 是自振频率为
是自振频率为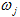 , 阻尼比为
, 阻尼比为 的单质点系在地面加速度
的单质点系在地面加速度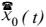 影响下的动力系数, 要注意各个质点的动力系数并不在同一时刻出现, 一般是在不同时刻出现, 所以在求最大内力时必须注意。
影响下的动力系数, 要注意各个质点的动力系数并不在同一时刻出现, 一般是在不同时刻出现, 所以在求最大内力时必须注意。
5 . 3 弹塑性体系的爆破地震反应 K
上面讨论结构在爆破地震作用下的振动反应时(图 4) , 是假定恢复力与位移成正比 , 即弹性阶段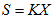 。
。
实际上结构在破坏以前 ,已进入塑性 ,所以应讨论弹塑性体系 ,
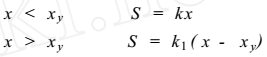
但是 ,影响爆破地震效应的因素基本相同 ,只是影响程度将不同。
5 . 4 岩土工程和地下工程对爆破地震效应的反应
对于位于地面以下的岩土工程(例如边坡) ,其反应与震害与地面上的建筑结构不同 ,它直接由地震波中的应力来决定。
地震波中岩土介质的应力有下式表示:
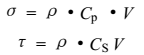
当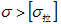 , 岩土介质就出现拉裂缝;
, 岩土介质就出现拉裂缝;
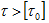 , 岩土介质就出现滑移。
, 岩土介质就出现滑移。
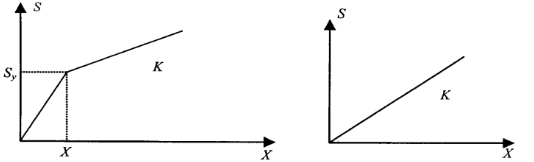
图 4 结构弹塑性体系的恢复力与位移关系
所以 ,此时地震荷载不是由地面运动最大加速度决定 ,而是由地面运动最大速度决定 ,当然还要由岩土介质特性决定。
6 结 语
震动运动方程式(1) 、式(7) 等价 ,结构的震动效应完全相同。因此 ,国内外爆破震动安全判据既有速度 ,也有加速度。考虑到地震加速度最大值主要反映高频成分的振动 ,而岩土工程的爆破地震效应反应由地面运动最大速度决定 ,作为统一 ,采用爆破震动地面运动最大速度为爆破震动安全判据是最佳的。
还应指出 ,材料的允许应力或材料的应力强度极限是与加载速率有关 ,这又和地运动的波形或频率成份有关。
应加强爆破震动持续时间对结构累积损伤破坏以及爆破震动频率对结构爆破震动安全标准影响研究。

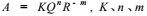 为常系数。
为常系数。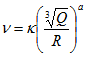
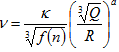 ,K,a为岩石特性等因素有关的常数 ,采用地震动最大加速度的经验公式亦为 ,
,K,a为岩石特性等因素有关的常数 ,采用地震动最大加速度的经验公式亦为 , 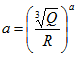 。
。
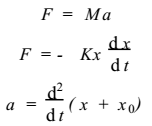
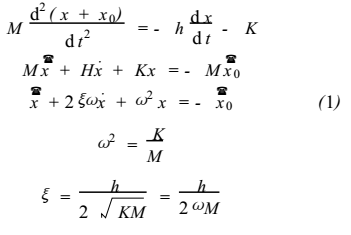
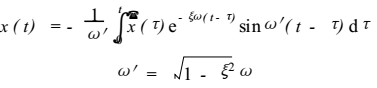
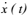 和绝对加速度
和绝对加速度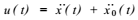 分别为
分别为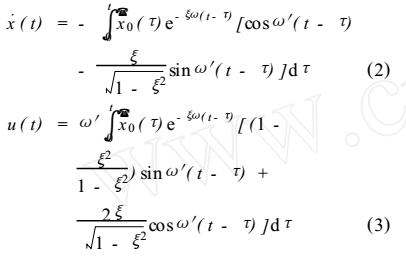
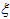 很小
很小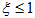 ,则在式(2)、式(3)中略去
,则在式(2)、式(3)中略去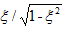 和
和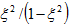 项,并取
项,并取 ,得到:
,得到:
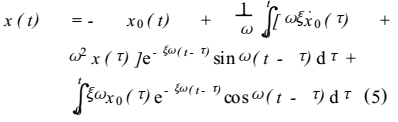

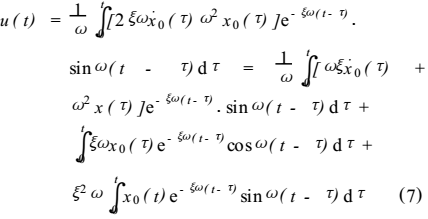
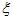 的高次项
的高次项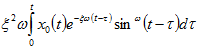 ,从而,在速度荷载激励下结构的相对位移为:
,从而,在速度荷载激励下结构的相对位移为:

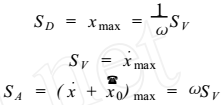
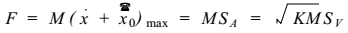
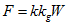


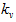 为速度地震动系数;
为速度地震动系数; 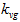 为速度动力系数。
为速度动力系数。
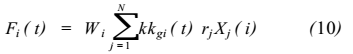
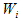 是第 i 个质量的重量; K 是地震系数;
是第 i 个质量的重量; K 是地震系数; 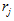 是振型分解系数。
是振型分解系数。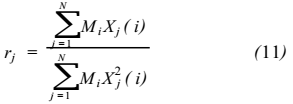
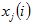 第 j 个振型 i 点处相对位移的值。
第 j 个振型 i 点处相对位移的值。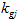 是自振频率为
是自振频率为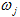 , 阻尼比为
, 阻尼比为 的单质点系在地面加速度
的单质点系在地面加速度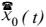 影响下的动力系数, 要注意各个质点的动力系数并不在同一时刻出现, 一般是在不同时刻出现, 所以在求最大内力时必须注意。
影响下的动力系数, 要注意各个质点的动力系数并不在同一时刻出现, 一般是在不同时刻出现, 所以在求最大内力时必须注意。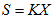 。
。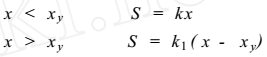
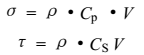
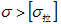 , 岩土介质就出现拉裂缝;
, 岩土介质就出现拉裂缝;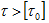 , 岩土介质就出现滑移。
, 岩土介质就出现滑移。