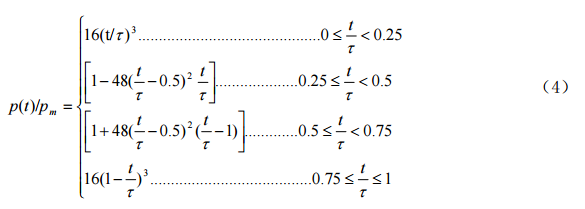杨 伟 林
( 江苏省地震工程研究院,南京 210014 )
摘要:本文采用波动有限元分析方法,研究复杂场地条件下工程爆破时场地的地震动效应,研究爆破地震动特征及衰减规律。根据某重点工程场地岩土参数的原位测试和试验结果,用自行研制的软件包进行场地爆破地震动效应的数值模拟分析,为工程爆破设计及施工前建筑
物、仪器设备的加固提供了依据。施工试爆实测结果与本文数值模拟分析给出的结果一致,说明本文方法是可行的。
关键词:爆破;地震动效应;有限元方法;数值模拟分析;试验
1.引言
交通、矿山、水利、城建等工程建设中,经常遇到爆破问题。工程爆破时,从爆源形成的振动以波的形式向周围传播,并引起周围介质的振动,这种振动称为爆破地震动,其强度随爆心距的增加而逐渐衰减。当爆破地震动达到一定强度时,就会引起地表和周围建(构)筑物、仪器设备等的不同程度的破坏。
爆破地震动效应主要研究爆破引起的地震动衰减规律及对周围建(构)筑物的影响等。在上世纪二十年代,国外的研究者就开始了这方面的研究,尤其是五十年代以后,随着地下核试验的开展和核防护工程的修建,以及工程爆破广泛应用,国内外研究者进行了一系列的理论模拟分析及试验研究,取得了比较大的进展[1 , 2]。归纳起来主要有两种途径:第一种途径是根据工程爆破经验,寻求爆破地震动减及对建筑物破坏的一般规律,在此基础上选择合适的爆破方式和爆破药量,确定爆破安全距离;第二种途径是根据爆炸力学及动力学理论,采用合适的模型及参数进行数值模拟分析,研究爆破产生的地震动效应,为工程爆破设计提供依据。
由于爆破场地介质特性、传播途径、局部地质条件等因素的影响,不同的经验公式间与场地有关的系数变化较大[2 , 3]。当工程爆破施工还未开始时,第一种途径给出的结果对特定的工程场地来说可能存在较大差异;第二种途径受数学、力学模型、介质参数,以及波动过程过于复杂等因素制约,也往往难以给出满意的结果。
本文结合国家某重点工程项目进行爆破地震动效应的数值模拟分析,将两种途径有机结合起来,采用波动有限元分析方法研究工程爆破时场地的地震动效应,研究爆破地震动衰减规律,根据具体工程场地的个别爆破实测数据对计算模型进行检验和参数优化,给出不同装药量及不同爆破方式时的爆破地震动预估值,为工程爆破设计及建筑物、仪器设备加固设计提供依据。爆破地震动效应数值模拟分析如图1 所示。工程施工时试爆实测结果与本文数值模拟分析得到的结果基本一致,说明本文方法是可行的。
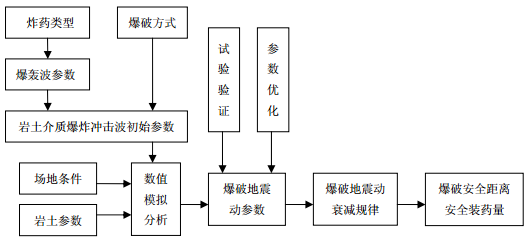
图 1 爆破地震动效应数值模拟分析框图
2. 爆破地震动效应研究的波动有限元分析模型
爆破时震源的震动能量是以波动形式向外传播的,爆破地震动过程实质上就是一个波动过程。当场地存在局部不规则地形、局部地质构造以及介质横向不均匀时,波在介质中的传播过程十分复杂,这类问题称为波的散射问题,因其介质的非均匀性,解析法的应用非常困难,在理论上至今还没有一种成熟的方法可直接应用。因此,横向非均匀介质内波动问题的数值分析方法日益为研究者所重视,如有限单元法(FEM)、有限差分法(FDM)及边界单元法(BEM)等,以它们的灵活、方便,而在工程中得到了广泛应用。这些方法将介质的波动方程转化为代数方程,使波动方程的求解大为简化,适用于解决较大尺度的具有复杂几何边界及物理介质面的波动问题[4]。
波动有限元分析方法将所研究的介质横向不均匀区域及边界区离散化,则连续非均匀介质的波动问题转化为如下离散系统的运动方程:

式中,M、C、K 分别为离散系统的质量矩阵、阻尼矩阵及刚度矩阵;
 分别为节点加速度列阵、速度列阵及位移列阵;R 为爆破产生的荷载列阵。
分别为节点加速度列阵、速度列阵及位移列阵;R 为爆破产生的荷载列阵。 在数值模拟分析中,计算域的选取及计算域边界处理尤为重要。人工边界是人为划定的计算区边界,在边界节点上需进行特殊处理,以符合波的实际传播特征。目前,用于处理人工边界的近似方法很多,这些方法实质上都是波外传过程的近似模拟。廖振鹏院士等在离散模型上直接模拟波的传播过程,提出了多次透射边界的概念,并应用于有限元法及有限差分法,有效地解决了人工边界区波的传播问题,取得了满意的效果[5]。
本文采用二阶透射边界方法,将介质横向不均匀区及人工边界区离散化,在任意时刻 t,先计算所有内点含入射波及散射波的总波场,边界区内用叠加原理扣除入射波场的影响,求出向外传播的散射波场,并外推人工边界下一时刻 t +Δt 的散射波场值。然后,将人工边界 t +Δt 时刻的散射波场和边界入射波场叠加,得到 t +Δt 时刻人工边界的总位移场,求出计算区内波动问题的散射波场及爆破地震动的总位移场,进而可求出其它感兴趣的量,如速度场、加速度场及应力场等。本方法能较好地模拟边界波的外传,提高计算结果的精度。
3. 爆轰波初始参数
研究介质的爆破地震动效应,首先必须根据所选定的炸药类型及爆破方式确定爆轰波的初始参数。
对固态和液态的凝聚炸药,实际应用中涉及的两个主要爆轰参数是爆速 VDJ 和爆压 PJ,两者之间关系可表示为[6]:
Pj=1/1+Kρ0V²DJ ⑵
式中,ρ0为炸药装药密度; k 为爆轰产物总绝热指数,一般情况下,k 可取为 3。则:
Pj=1/4ρ0V²DJ ⑶
不同炸药的爆轰参数相差较大,高爆炸药的爆速高达 6000—9000m/s,而低爆速炸药的爆速仅 1500—2000m/s 左右。在控制爆破中,为了使爆破能量得到合理利用并减轻爆破的危害作用,常采用低爆速炸药或不偶合装药以及微差爆破等方式来控制爆破,以期减轻爆破地震动对周围建、构筑物可能产生的不利影响。
炸药爆炸时对岩土介质产生的是一个脉冲压力波,脉冲压力波的形状与装药密实度、不耦合系数等有关。数值模拟计算中,将爆压 p(t)、时间 t 按 p(t)/pm、t/τ进行归整后,单炮脉冲压力波时程近似用下式表示:
式中,τ为脉冲宽度(毫秒),pm 为爆轰波对岩土介质的爆压最大值(GPa)。当采用微差爆破时,脉冲时程为多个单炮脉冲时程叠加。
为了确定单炮脉冲时程宽度,对国内一些爆破地震动的记录进行了分析,这些爆破记录的爆破药量从数公斤至近千吨不等,爆心距最近的仅几米远,最远的约 500 米。根据爆破地震记录分析,观测点地面震动从开始至振幅最大值发生的时间间隔,最小的为 17 毫秒,最大的为 40 毫秒。本文数值模拟计算中,根据初步爆破施工方案,计算单炮脉冲宽度取 25 毫秒。
4. 工程概况及岩体参数
4.1 工程概况
国家某重点工程施工过程中需进行石方明挖爆破,爆破点距国家通讯干线的一个微波通讯站最近处仅 60 米左右。该微波通讯站建于上一世纪 70 年代,为半地下框架结构,站内部分设备老化,通讯设备对振动比较敏感。
为防止施工时爆破产生的地震动导致微波站建筑结构及仪器设备的损坏,需对场区爆破地震动效应进行研究,确定爆破安全距离及安全装药量, 为工程进入施工阶段时确定爆破对微波站可能产生的影响及爆破安全距离提供预估值,并为本工程的爆破设计及确定爆破施工工期提供参考数据。
4.2 场地条件
所研究的工程场地为一不规则形状的短浅沟源坳地,高程 420—527 米,是典型的构造—剥蚀地貌,场区构造较为复杂。根据钻探、物探以及平硐所揭示的地质条件,场区岩体以花岗斑岩和石英砂岩为主,夹少量粉砂质泥岩和泥质粉砂岩。
4.3 岩体参数
经现场原位测试和试验室试验,岩体的物理力学指标见表 1。采用地震折射法、平硐地震弹性波测试、钻孔声波测试、跨孔弹性波 CT 探测方法进行场区岩体弹性波速测试。综合四种方法的测试结果分析,场区岩体的弹性波速以大于 3500m/s 为主,下部弱风化砂岩的波速大于 4000m/s,破碎带及强风化花岗斑岩和弱风化泥岩的弹性波速为 2000—3000m/s。
表 1 岩体物理力学指标
| 岩石名称 |
风化程度 |
重度(KN/m³) |
抗压强度(MPa) |
弹性模量(×10^MPa) |
| 石英岩状砂岩 |
微风化 |
25.71 |
145 |
7.22 |
| 石英岩状砂岩 |
弱风化 |
25.5 |
83 |
6.75 |
| 岩屑石英砂岩 |
弱风化 |
25.5 |
54 |
5.21 |
| 细砂岩 |
弱风化 |
25.44 |
38 |
4.15 |
| 泥质粉砂岩 |
弱风化 |
25.2 |
22 |
3.64 |
| 粉砂质泥岩 |
弱风化 |
25.5 |
22 |
4.14 |
| 花岗斑岩 |
微风化 |
25.46 |
108 |
5.95 |
| 花岗斑岩 |
弱风化 |
25.14 |
41 |
3.70 |
| 花岗斑岩 |
强风化 |
22.06 |
12 |
1.87 |
5. 试验验证及参数优化
在本工程局部施工爆破中,业主曾进行爆破振动测试,在微波通讯站办公及仪器房内布置了 2 个测点,测点距爆破点约 300 米,共进行了三次爆破,爆破药量分别为 30kg、48kg 和 66kg。
为了检验及优化爆破地震效应计算中所采用的参数,根据爆破地震动实测数据进行对比分析。因爆破药量为 30kg 及 48kg 时,实测振速较小,采用爆破药量 66kg 时的振速实测数据进行对比验证。采用自行研制的“爆破地震效应分析软件包 ESELand(V1.2)”进行数值模拟计算,整个计算区长 700 米,爆轰波脉冲宽度取为 25 毫秒,模拟计算结果与实测结果列于表 2。
从计算结果与实测数据的对比可知,两者是基本吻合的,这说明进行爆破地震动模拟分析中所采用的参数基本可行。
表 2 爆破地震动实测数据与模拟计算结果对照表
| 物理量 |
实测数据 |
计算值 |
| 1#点 |
2#点 |
平均 |
| 径向 |
速度(cm/s) |
0.043 |
0.045 |
0.044 |
0.041 |
| 加速度(g) |
|
|
|
0.008 |
| 竖向 |
速度(cm/s) |
|
|
|
0.046 |
| 加速度(g) |
|
|
|
0.010 |
| 最大速度(cm/s) |
0.045 |
0.046 |
6.爆破地震动衰减规律
6.1 一般形式
爆破时,场地的地震动强度与爆破采用的药量、爆破方式、爆心距、场地条件及所爆破的岩土介质特性有关。为了确保周围建、构筑物的安全,需根据不同装药量、不同爆心距时实测的爆破地震动速度及加速度值,进行回归分析,研究场地的爆破地震动衰减规律,为工程爆破设计提供依据。
目前,工程界通常采用如下形式的爆破地震动衰减公式:
A=KQ^nR^-m ⑸
式中:A 为爆破地震动幅值(可为位移、速度及加速度);Q 为爆破药量;R 为爆心距;K、n、m 为与场地条件、传播途径及介质特性等有关的常数,由实测数据回归得出。
国内外众多学者根据各自的实践经验,提出了许多经验公式。这些经验公式因场地条件、传播途径及介质特性等差异较大,在应用上均有一定的局限性。根据多年实践经验,本文采用式(6)所示的爆破地震动衰减公式:
A=K(³√Q/R)^ α ⑹
式中:Q 为装药量;R 为爆心距;K、α为回归常数;A 为地震动幅值(速度、加速度或位移)。
目前,许多工程及研究单位采用式(6)形式,我国《爆破安全规程》也推荐采用式(6)计算爆破地震动强度、爆破安全距离及安全装药量[7]。对不同场地,所不同的仅是与场地条件、传播途径及介质特性等有关的常数 K、α存在差异。
6.2 数值模拟分析
为了确定本工程场地的爆破地震动衰减规律,进行爆破地震动数值模拟分析,爆破药量分别为 30kg、48kg 和 66kg,爆心距 35m—215m。本工程需大量石料,高爆速炸药易使岩体破碎,块石采集率降低,爆破施工中采用低爆速炸药。计算中,炸药的爆速取为 2000m/s,所研究场地各计算点的爆破地震动速度及加速度见表 3。
表 3 爆破地震动计算结果
| 药量(kg) |
爆点高程(m) |
计算点序号 |
高程(m) |
爆心距(m) |
竖向 |
径向 |
| 速度(cm/s) |
加速度(g) |
速度(cm/s) |
加速度(g) |
| 66 |
460 |
1 |
518 |
215 |
0.285 |
0.078 |
0.551 |
0.157 |
| 2 |
515 |
195 |
0.406 |
0.125 |
0.667 |
0.161 |
| 3 |
499 |
160 |
0.400 |
0.072 |
0.640 |
0.143 |
| 4 |
485 |
115 |
0.679 |
0.115 |
1.033 |
0.199 |
| 5 |
474 |
85 |
0.953 |
0.199 |
1.501 |
0.262 |
| 6 |
468 |
60 |
3.904 |
0.851 |
3.600 |
0.610 |
| 7 |
468 |
45 |
6.973 |
1.138 |
6.234 |
0.823 |
| 8 |
468 |
35 |
11.97 |
2.095 |
10.13 |
1.559 |
| 48 |
460 |
1 |
518 |
215 |
0.212 |
0.059 |
0.400 |
0.121 |
| 2 |
515 |
195 |
0.299 |
0.065 |
0.479 |
0.120 |
| 3 |
499 |
160 |
0.361 |
0.068 |
0.560 |
0.113 |
| 4 |
485 |
115 |
0.502 |
0.095 |
0.779 |
0.157 |
| 5 |
474 |
85 |
0.828 |
0.153 |
1.213 |
0.196 |
| 6 |
468 |
60 |
2.486 |
0.608 |
2.587 |
0.494 |
| 7 |
468 |
45 |
4.633 |
0.812 |
4.572 |
0.658 |
| 8 |
468 |
35 |
8.009 |
1.595 |
6.865 |
1.211 |
| 30 |
460 |
1 |
518 |
215 |
0.159 |
0.041 |
0.287 |
0.063 |
| 2 |
515 |
195 |
0.200 |
0.046 |
0.306 |
0.072 |
| 3 |
499 |
160 |
0.256 |
0.051 |
0.386 |
0.079 |
| 4 |
485 |
115 |
0.406 |
0.078 |
0.639 |
0.132 |
| 5 |
474 |
85 |
0.666 |
0.132 |
0.937 |
0.167 |
| 6 |
468 |
60 |
1.692 |
0.389 |
2.108 |
0.425 |
| 7 |
468 |
45 |
3.107 |
0.518 |
3.757 |
0.566 |
| 8 |
468 |
35 |
4.000 |
1.030 |
4.832 |
1.080 |
利用表 3 数据按式(6)进行回归分析,得到进行本工程场地爆破地震动衰减规律:
V=314.7(³√Q/R)^1.67 ⑺
式中:Q 为单孔装药量,单位为 kg;R 为爆心距,单位为 m; V 为爆破震动速度峰值,单位为 cm/s。
本工程原方案采用单孔装药量 60kg、微差爆破的施工方式。按该方案,在爆点距微波站建筑物距离最近时(约 60 米),数值模拟计算及按回归公式(7)得到的微波站场地爆破地震动速度及加速度见表 4。从表中可看出,爆破引起的地震动速度达 3.1cm/s,按式(7)计算结果为 3.30cm/s,两者基本相同。按照 GB6722-2003《爆破安全规范》,这一振动对抗震性能较好的框架结构来说是安全的。但因微波站设备老化、抗振要求高,在对设备进行隔振、隔冲设计前,原爆破施工方案是不可行的,应按照所确定的工程场地爆破地震动衰减规律,根据爆破允许震速[V]确定爆破安全距离及安全装药量。
表 4 爆破地震动对微波站场地的影响(药量 60kg,爆心距 60 米)
| 方向 |
物理量 |
数值模拟计算 |
回归公式 |
| 径向 |
速度(cm/s) |
2.97 |
|
| 加速度(g) |
0.51 |
|
| 竖向 |
速度(cm/s) |
3.10 |
|
| 加速度(g) |
0.59 |
|
| 最大速度(cm/s) |
3.10 |
3.30 |
6.3 试爆实测结果
为了验证数值模拟分析得到的爆破地震动衰减规律的可靠性,在正式施工前进行了试验爆破。爆破药量分别为 5kg、10kg、20kg、76kg,爆点高程分别为 504.0m、497.6m、497.8m、440.6m,爆心距为 13—152.4m,爆破点与测点的高程差为 2.1—22.4m。试爆实测结果见表5。根据实测数据按式(6)回归得到的回归常数 K、α分别为 165.5、1.688,方差σlgv 为 0.194,实测数据与回归结果的相对关系见图 2。
从图中可看出,实测数据的上包络线为回归结果加上 1.5 倍方差,按此计算得到的爆破地震动衰减规律为:
V=323.7(³√Q/R)^1.688 ⑻
对比式(7)、式(8)参数可知,参数 K、α的差异分别为 2.8%、1.1%,两者差异很小,这说明数值模拟分析得到的爆破地震动衰减规律与施工试验爆破时实测数据回归结果基本一致,本文方法是可行的。
表 5 试爆实测振动速度
| 测点 |
高程m |
5kg |
10kg |
20kg |
76kg |
| 爆心距m |
速度cm/s |
爆心距m |
速度cm/s |
爆心距m |
速度cm/s |
测点 |
高程m |
爆心距m |
速度cm/s |
| 1-1 |
506.1 |
13 |
10.50 |
26 |
1.31 |
28 |
2.50 |
2-1 |
446.0 |
50 |
4.12 |
| 1-2 |
507.8 |
25 |
2.23 |
40 |
1.45 |
40 |
0.80 |
2-2 |
447.0 |
90 |
1.87 |
| 1-3 |
511.0 |
48 |
0.66 |
59 |
1.02 |
58 |
0.47 |
2-3 |
450.8 |
152 |
0.35 |
| 1-4 |
515.9 |
80 |
0.35 |
90 |
0.40 |
85 |
0.27 |
|
|
|
|
| 1-5 |
520.0 |
106 |
0.20 |
120 |
0.16 |
112 |
0.17 |
|
|
|
|
| 1-6 |
520.0 |
116 |
0.19 |
120 |
0.18 |
111 |
0.26 |
|
|
|
|
图 2 爆破实测数据回归结果
7. 结束语
爆破引起的振动达到一定强度时,将导致周围建(构)筑物和仪器设备损坏,需对爆破引起的场地地震动效应进行研究,确定爆破安全距离和安全装药量。受场地条件、传播途径及介质特性等差异的影响,不同场地的爆破地震动衰减特征存在较大差异,现有的一些经验公式在应用上往往有一定的局限性。
本文采用波动有限元方法进行复杂场地条件下爆破地震动效应的数值模拟分析,该方法可充分考虑具体工程场地复杂的地形地貌、局部地质构造等的影响,为爆破施工前文物保护和重要建(构)筑物、仪器设备的加固及工程爆破设计提供参考依据。工程施工时试爆实测结果与本文数值模拟分析给出的结果基本一致,说明本文方法是可行的。


 分别为节点加速度列阵、速度列阵及位移列阵;R 为爆破产生的荷载列阵。
分别为节点加速度列阵、速度列阵及位移列阵;R 为爆破产生的荷载列阵。