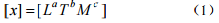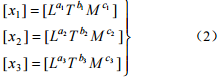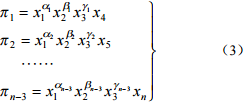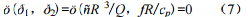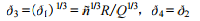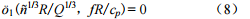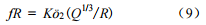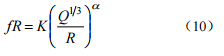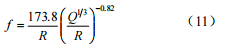关键词:爆破振动;主振频率;量纲分析;预测;回归分析
引 言
爆破振动作为爆破作业带来的必然结果,在一定程度上威胁着爆区附近建(构)筑物的安全。为避免对建筑物造成结构性破坏,长期以来,国内外研究人员通过理论和监测分析,对爆破振动的衰减规律及建筑物的爆破振动破坏标准进行了大量的研究。对衡量爆破振动强度的物理量与建筑物破坏程度的相关性统计分析的结果表明,质点振动速度与建筑物破坏程度的关系最为密切[1]。因此,以单一的质点振速峰值作为爆破振动安全的评定标准在国内外得到了广泛应用,不同的国家对不同类型的建(构)筑物制定了相应的安全标准[2,3]。
但是,近年来的一些爆破震害观测和分析表明,建筑物的破坏不仅取决于质点振速峰值,而且和振动频率和持续时间密切相关。针对单一的振速峰值安全判据存在的缺陷和不足,目前,一些国家在制定新的爆破振动安全判据时,普遍考虑了振速与频率的共同影响[4,5]。
尽管人们已经充分认识到频率在爆破震害中的重要作用,但目前关于爆破振动衰减规律的预测研究仍以振速峰值为主,而对于频率的研究则很少。因此,通过实测数据对爆破振动频率进行预测研究,对于了解和掌握爆破振动频率的衰减规律、降低爆破振动的破坏效应具有非常重要的意义。
1 量纲分析法的基本原理
量纲分析法是应用量纲和谐原理探求物理现象中物理量之间的函数关系,即建立物理方程(相似准数方程)的一种方法。特别是对于某些复杂的实际问题,当不能事先用方程分析的方法建立描述现象的方程式时,量纲分析法是求得相似准数的唯一方法。
1.1 量纲和谐原理量纲是物理量的广义量度单位,它分为基本量纲和导出量纲。质量系统常用的基本量纲是:长度[L]、时间[T]、质量[M]。任一物理量 x 的量纲公式可以用基本量纲的指数乘积形式来表示。即
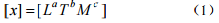
式中,a、b、c 为基本量纲的指数。当 a、b、c 有一个不为零时,称 x 为有量纲的量;当 a、b、c 全为零时,即[x]=[LºTºMº]=[1],称 x 为无量纲量或无量纲数。
根据物理学的量纲分析,只有量纲相同的物理量才能相加减。因此,任何一个正确、完整的物理方程式中各项的量纲必须一致,这种性质称为量纲和谐原理。
1.2 ð 定理
ð 定理作为量纲分析的一种常用方法,其具体内容是:假设表示某一物理过程的函数式中包含 n个物理量[Ö (x1,x2,…,xn)= 0]其中基本量纲 m个,则该物理过程可由 n 个物理量组成的(n~m)个无量纲量的关系式[ö(ð1,ð2,…,πn~m) = 0]来表示。在应用 ð 定理建立物理方程时,可以按下述方法来选取基本量纲和 ð 项组合[6]:
(1)从 n 个物理量中选取 m 个不能组合成无量纲量的基本物理量来代表 m 个基本量纲(一般m=3)。基本物理量 x1、x2、x3的量纲公式可表示为
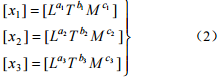
x1、x2、x3 不能组合成无量纲量的条件是量纲公式中的指数行列式不等于零。
(2) ð 项组合可以由三个基本物理量和其他的物理量依次组合而成。即
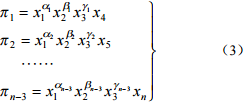
式中,ái、âi、ãi 分别为各 ð 项的待定指数。这些指数可以根据[π1]=[LºTºMº]来进行求解。
2 相似准数方程的建立
对爆破振动这种具有瞬态特性的随机信号,由于振动过程和影响因素非常复杂,要想全面考虑各种因素来建立爆破振动频率的相似准数方程非常困难。但大量的观测分析结果表明,在一定的爆破方式下,药量和爆源位置对频率的影响最大,而爆区地质条件、岩石性质和局部场地条件对频率也具有较大的影响。因此,可选择段最大药量(Q)、爆心距(R)、岩石中的纵波速度(cp)和岩石密度(ñ)作为影响爆破振动频率(f)的主要物理量。则 f 与Q、R、cp 和 ñ 之间的函数关系可表示为
Ö( f,R,Q,cp,ñ)= 0 (4)
选取 R、cp、Q 作为基本物理量,则有


根据量纲和谐原理对 ð1、ð2的待定指数求解后,有
ð1 = ñR³/Q,ð2 = fR/Cp
由此得到无量纲量所表达的关系式为
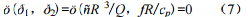
为了在形式上与常用的质点振速峰值预测公式保持一致,取新的 ð 项组合为
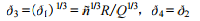
则式(7)可改写为
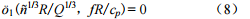
因此,爆破振动频率的相似准数方程可表示为
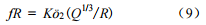
式中,K 是与 ñ 和 cp 有关的系数,即 K = K(ñ,cp)。
3 主频率预测的回归分析
华能汕头电厂二期主厂房基坑采用爆破方法进行开挖。由于开挖基坑紧邻一期主厂房,为避免爆破振动对一期主厂房和厂房内的控制仪器、设备和开关,以及汽轮机造成危害,北京科技大学受华能汕头电厂的委托,承担了爆破振动监测任务。
3.1 爆破施工及监测概况
爆破开挖采用小台阶浅眼爆破法,孔径 42 mm,孔深 2.5 ~ 4.8m。为减少爆破次数和钻眼数量,采用扩壶孔和连续装药孔联合布孔方式。选用 2#岩石炸药和非电 ms 雷管起爆。
监测仪器采用美国 SAULS 公司生产的NCSC5000 型测振仪和北京矿冶研究总院生产的DSVM-4C 型振动测试仪。共布置两条监测线:1# 测线为地面监测线;2# 测线为主厂房 15 m 监测线(距地面高度为 15 m)。
通过对 57 次爆破(总药量 6.4 ~ 254 kg,单段最大药量 1.2 ~ 75 kg,0.02≤Q1/3/R≤0.25)的振动监测,共得到 313 个测点的实测振速波形。其中,1# 测线 201 个,2# 测线 112 个。
3.2 主频率预测公式的回归分析
由于爆破振动的频率特性在很大程度上是由最大振幅所对应的频率,即主振频率所决定的。根据所建立的爆破振动频率相似准数方程,假设地面质点爆破振动主频率的预测公式具有如下形式
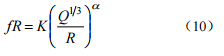
式中,K、á 是与爆区地质条件、介质性质和局部场地条件等有关的系数。
利用 1# 测线 DSVM-4C 型测振仪测得的垂直向振速波形(185 个测点)采样后求得的主振频率和Q、R 值对式(10)进行线性回归计算,得到 K =173.8,á = -0.82,其线性相关系数ã = 0.84(回归直线如图 1)。因此,现场爆破条件下主振频率的预测公式为
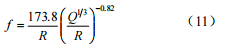

图 1 主频率与比例药量的线性回归结果
从回归分析得到的主频率预测公式和图 2 可以看出:当 R 为定值时,主频率随 Q 的增大而降低;当 Q 为定值时,主频率随 R 的增大而降低;当比例药量不变时,主频率随 R 的增大而降低。这和目前关于爆破振动频率衰减特性的研究结果相吻合。

图 2 主频率与 Q、R 的关系曲线
4 结 论
(1)通过用量纲分析法建立爆破振动频率的相似准数方程,并对实测波形的主振频率进行回归分析,得到了特定爆破条件下主频率的预测公式;
(2)得到的主频率预测公式在表达形式上与振速公式一致,并具有明显的物理意义,而且和目前关于爆破振动频率衰减特性的研究结果相吻合。
(3)对于其他爆破条件下的主频率进行预测时,K、á 的取值需要做进一步研究。